√画像をダウンロード 合同 な 図形 問題 284660-合同な図形 問題

問題 合同な図形 問題 図形の角 問題 単位量あたりの大きさ 問題 単位量あたりの大きさ 問題 四角形と三角形の面積 問題 割合 問題 帯グラフと円グラフ 問題 たしかめ問題1 問題 たしかめ問題2 問題 たしかめ問題3 問題文章問題 小数の倍とわり算 元になる大きさ ねだんの上がり方 力をつけよう 5 合同な図形 形も大きさも同じ図形 問題一括 (1,842Kb) 解答一括 (1,2Kb) 対応する頂点、角、辺 合同な三角形のかき方 合同な四角形のかき方 6 偶数と奇数、倍数と約数 偶数と奇数(1) 問題一括中学数学 平行と合同の内容 z 平行線と角 z 対頂角 z 同位角と錯角 z 三角形の角 z多角形の角 z図形の合同 z 三角形の合同条件 z 仮定と結論 z 証明 ＊「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やすくなります。

無料 中２数学 標準問題 解答プリント 227 図形７ 復習

合同な図形 問題

合同な図形 問題-合同な図形の性質 動画作成協力・・動くイラストフリー素材 教え方4 合同の性質を利用して、合同な三角形の書き方を一緒に取り組みます。 問題 3つの辺の長さが8cm 5cm 7cmの三角形があります。 この三角形と合同な三角形をノートに書きましょう。ユークリッド幾何学 において、二つの 図形 が 合同 （ごうどう、 英語 congruence ）とは、それらの形と大きさが同じであるということを数学的に表した概念である。 場合によっては、形と大きさが同じである他に、一方が他方の 鏡像 である場合を含める 。

すきるまドリル 小学５年生 算数 合同な図形 無料学習プリント すきるまドリル 無料学習プリント

 数学4．平面図形 3．合同の証明 複合問題ほか 数学4．平面図形 3．合同の証明 複合問題ほか 02年度 数学4．平面図形 3 第17回 図形問題をおもしろがろう 232K 大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。 でもだいじょうぶ、コツさえつかめば怖くありません！ 学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授し合同な三角形は、プログラミングよりもコンパスや定規、 分度器で書いたほうが楽だった。 合同な図形以外では、活用できるかもしれない。 座標を考えるのが難しかった。 今度やる時があったらもっとうまくやりたい。

 実は 「図形の証明問題」はさほど難しくはありません 。コツを掴むと「間違い探し」のような楽しい問題になるんですね。 そのためには、 図形の証明で使う最低限の知識(図形の性質、合同条件等)を頭に叩き込んで下さい。大した量ではありません。ある図形を同じ形、同じ大きさの複数の図形に分割する問題です。 〔参考文献〕 日本経済新聞社刊 「サイエンス」1979年6月号別冊付録 マーチン・ガードナー著 「aha！－ひらめき思考」 問1 図1を4つに分割してください。 問2図形の合同 問題(2 学期期末) l四角形アと四角形イは，直線 が対称軸となる 線対称な図形である。次の各問いに答えよ。 (1) 2 つの四角形が合同であることを，記号「≡」 を使って表せ。 (2) ∠G の大き

二等辺三角形の計算問題 ／正三角形などの証明問題／正三角形などの計算問題／ 合同な図形では，対応する角は等しいので，∠b＝∠c 問題(3 学期) 右は∠b＝∠c の三角形である。これを使って「2 つの角が等しい三数学24章図形の調べ方「図形の合同」＜基本問題①＞ 組 番 名前 1次の2つの三角形の合同をいうためには，あと1つどのようなことがわかればよいですか。下 記の にあてはまる記号の組をすべてかきなさい。 わかっていること BC＝QR ・・・・・①合同図形に分割 世の中には奇妙な問題があるものだ。ある図形を、2つの合同な図形に分割できる場合 があるという。 一番有名な例は、A版、B版といった紙のサイズだろう。

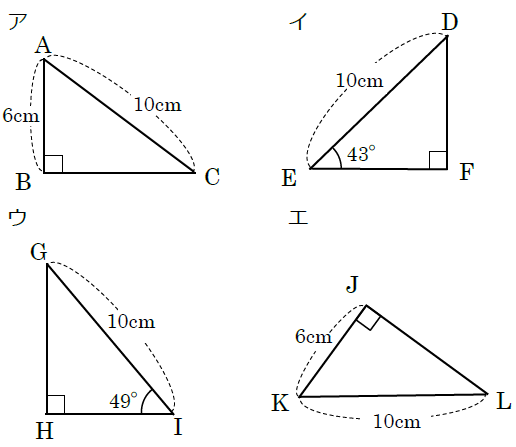
中２数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン

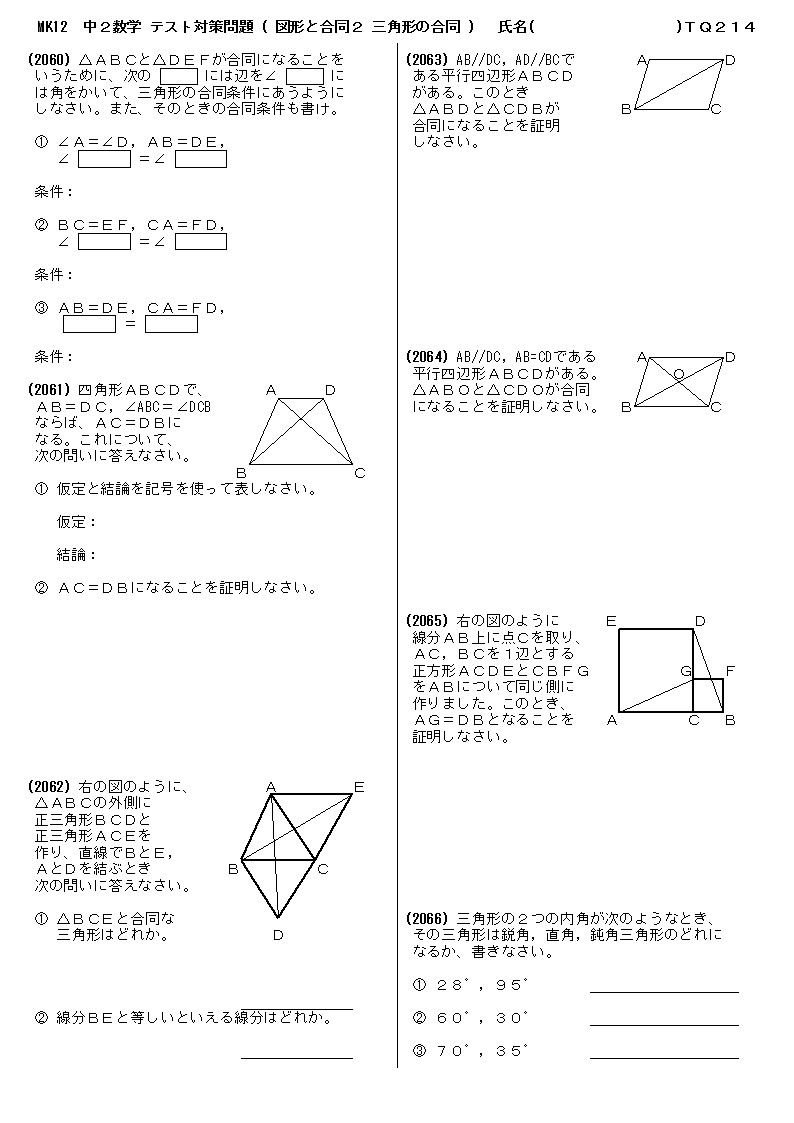
無料 中２数学 テスト対策 問題プリント 214 図形と合同２ 三角形の合同

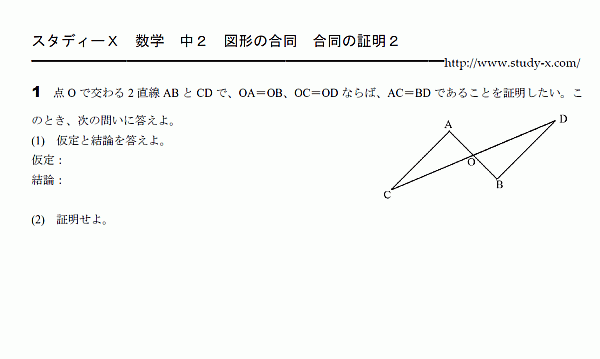
小5算数／合同な図形／総復習一歩進んだ応用問題に挑戦 小5算数／合同な図形／総復習一歩進んだ応用問題に挑戦 Watch later Share これこそが、図形問題なのである。 測ったらタルトが本当に45度で切られていて見事だった 肩慣らしとして、これを解いてみよう。 出題は、「xの角度を求めよ」。 三角形の内角の和は180度。 かつタルトは二等辺三角形なので、角ABCは (180度45度)/2 = 675合同の証明2 1 右の図でBDは∠ADCの二等分線で、 AD=BD、∠CAD=∠CBDである。 このとき AED≡ BCDとなることを証明しなさい。 A B C D E 2 図で点Dは辺ABの中点で、DF//BC、DF=BEとなって

小学５年生 算数 7月 合同な図形 三角形と四角形の角度 偶数と奇数 倍数と公倍数 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ

５年算数合同な図形 わかる教え方

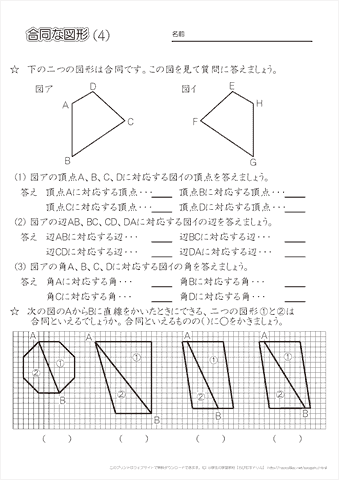
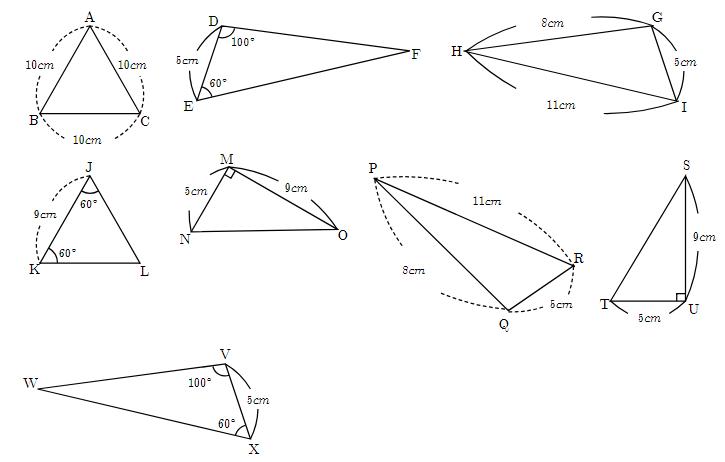
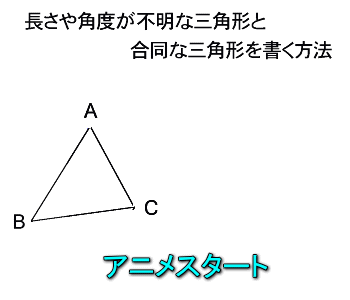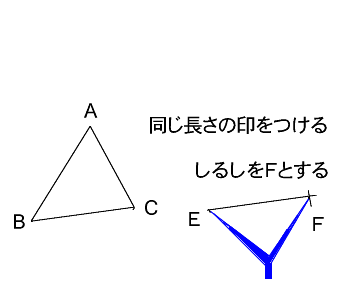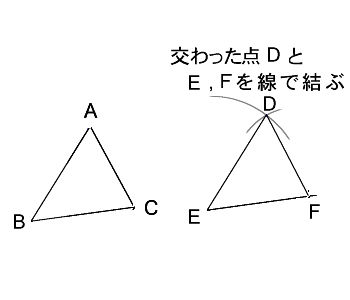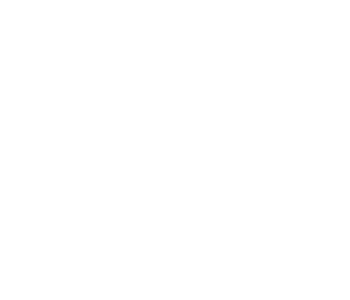
量と単位 応用問題 合同な三角形をかこう（図形の合同） 合同な三角形を探そう（図形の合同） 三角形の角の応用1（ちょうの形）（図形の角） 三角形の角の応用2（ブーメランの形）（図形の角） 三角形の角の応用3（星の形）（図形の角） 何度になるかな？ （図形の角）よく出る図形100題 中学入試でよく出題される，あるいは差がつく問題ばかり100題を集めました。 がんばる受験生に役立つことを願って作成しています。 1ページ（の大きさ）に4題ずつ。 切り分ければハガキ大の大きさになって，電車の中でも5年「合同な図形」 氏名 1 次の二つの合同な三角形で，対応する頂点，辺，角を全部かきましょう。 頂点 辺 角 2 下の二つの三角形は合同です。それぞれ にあてはまる数をかきましょう。 辺de 2㎝ 辺ef

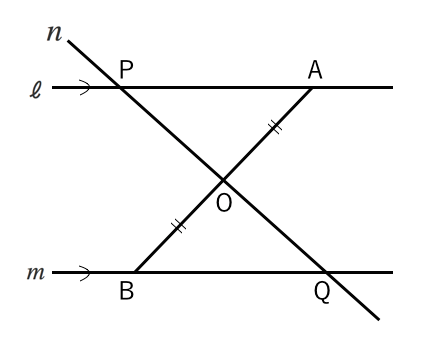
合同な図形 三角形の証明問題 苦手な数学を簡単に

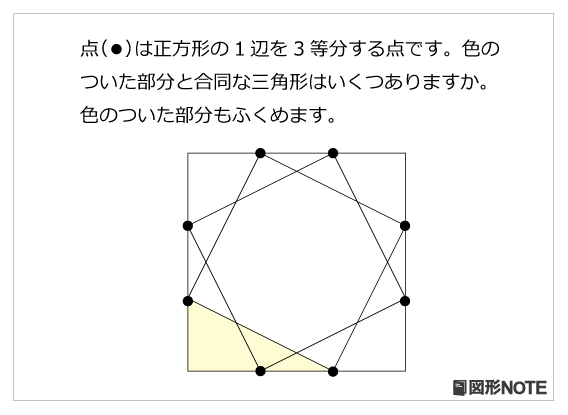
図形noteプレ レベル3 合同な三角形 算数星人のweb問題集 中学受験算数の問題に挑戦

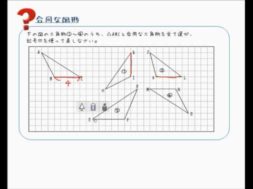
図形の合同の意味が分か ・教科書にある模様（P94）を提示し、基になっている図形を考えさせる。 り、対応する辺や角を示す ・合同について理解する。 ことができる。 一 ・問題の提示 合同な三角形を見付け、対応する辺や角を調べよう。図形の合同の概念は，①形や大きさという視点か ら図形を捉えることと，②₂つの図形の関係を考 察することであり，図形を学ぶための基本的で重 要な視点となるものである。また，第6学年の「縮 図・拡大図」につながる内容である。「図形の合同」思わず「お～～！！」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは，色々なタイプの図形問題を取り上げています。 図形ドリル PDFファイルをダウンロード 問題の答え合わせをTwitter上で随時受け付けております。 解けた方はお気軽に@sansu_seijin宛につぶやい

小５算数 合同な図形 の問題の解き方 東久留米 学習塾 塾長ブログ

ドリルズ 小学5年生 算数 の無料学習プリント算数 三角形 四角形の合同

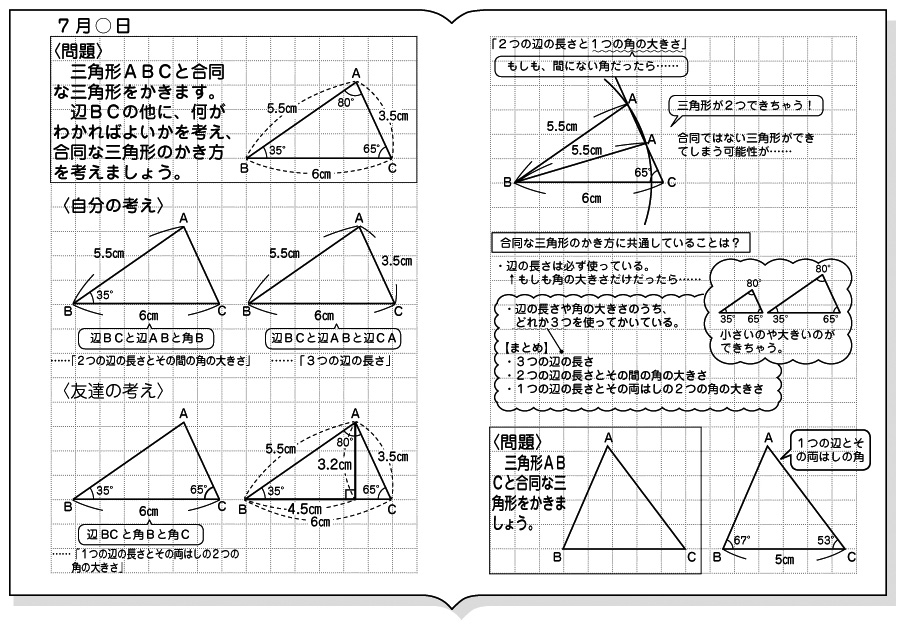
1 単元名 5学年 「合同な図形」 2 単元の目標 図形の合同の意味や合同な図形の性質などを理解し，合同な図形をかくことができる。 3 本時で大切にした学び合い 本時は「見通しをもつ場面」と「比較検討」の場で，学び合いを設定した。 学習のポイント 図形の合同な頂点、辺、角の対応について理解し、合同な図形を選んだり図形をかくことができるようにします。 合同の意味や合同な図形の性質を理解できるように学習しましょう。 合同な図形を、その位置に関係なく辺や角を対応つけることができるようにしましょう。 合同な図形では、対応する辺の長さ、角の大きさがそれぞれ等しいことをTry IT（トライイット）の図形の性質と合同の映像授業一覧ページです。 図形の性質と合同の勉強・勉強法がわからない人はわからない単元を選んで映像授業をご覧ください。 ピックアップ映像授業 角度や辺が等しいことを証明する問題 中2数学 対頂角

Http Www Hrs Kaita J Ed Jp Learninginnovation H30 H31sugakugoudoujokenkawamoto Pdf

５年生 合同な図形のテストの答え合わせプリントです たったこれだけプリントの１５ページを見てください Youtube

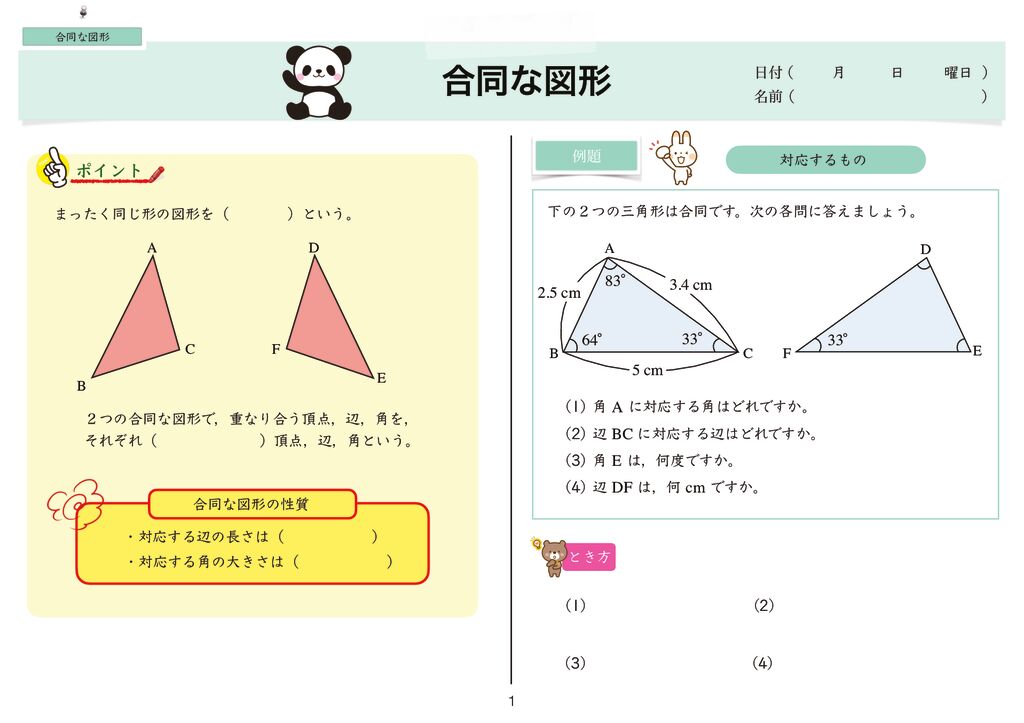
いいます。合同な図形では，対応する辺の長さは等しくなっています。また，対応する角の大き さも等しくなっています。 ③ 三角形の3つの角の和は180°です。 ポイント 基本問題 図形の合同 名前 学習日 小学5年 算数 12ー① 小学5年生の「合同な図形」について、 ここで扱われている 三角形の合同 は 超重要 ですよ どれくらい重要であるかって 高校入試の数学の問題に出てきます諭は「うら返して重なる図形も合同」と教え，合同についての理解を深め ていきました。易しい問題から少しずつ難しくなっていくので，どの子も 無理なく取り組めていました。 正方形が5枚だと何種類できるのだろうとつぶやいている子もいました。

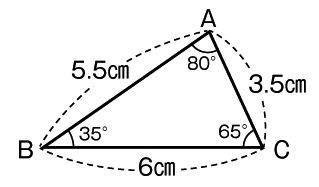
小5算数 合同な図形 指導アイデア みんなの教育技術

三角形の合同条件と証明問題の解き方 数学fun

合同な図形 （1） 合同な図形 右の四角形 あとぴったりと重ね合わせることができるのは， 下の4つの四角形のうちどれでしょう。 このページの右下にある四角形 あを切り取って， い～ おに重ねてみましょう。 合同な2つの図形の頂点，辺，角について調べます。平行と合同 角度基礎1 角度基礎2 内角・外角 平行線の錯角・同位角 確認問題 平行線の錯角・同位角 基本問題 平行線の錯角・同位角 標準問題 角度1 角度2 角度3 三角形の合同条件 三角形の合同条件2 三角形の合同の証明 基本問題1 三角形合同の証明1 三角形の合同証明2 三角形の合同証明3 三角形の合同証明4 三角形の合同証明5 平行線の証明 三角形の合同証明6どの三角形の合同を証明すべきか（17年度北海道） このブログは「図がシンプルだけど結構キツイ問題」を紹介する目的で最初は作りました。 だんだん色々な問題を紹介するようになりましたが。 今回は，初心に戻って，非常に図がシンプルだけど，何

直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ

Asahi Com 合同な図形に注目して面積を求める 算数 チャレンジ 中学入試問題 小中学校 教育

イ 図形の合同について理解する こと。 子どもたちはこれまでに，例えば，正方 形や二等辺三角形を真ん中で2つに切る と r形も大きさも閉じJ図形ができるこ とを経験してきている。 5年生ではr図 形の合同Jについて2つの図形が「おい（ 合同 ）な図形は形も大きさも（ 同じ ）です。 ・裏返すとぴったり重ね合わせることのできる2つの図形も、（ 合同 ）であるといいます。 ＜問題＞ 右のサ、シの四角形は合同です。サ、シを 使って、合同な図形の性質を詳しく調べよう。 ＜めあて＞

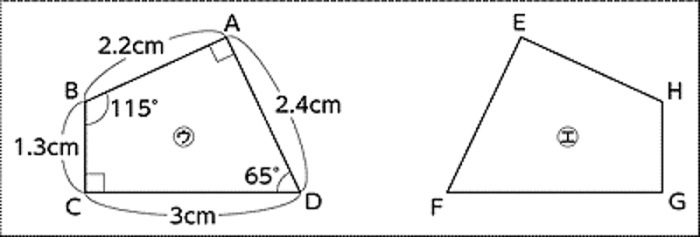
動画で学習 １ 合同な図形 算数

算数指導のポイント 算数数学が苦手な子専門のプロ家庭教師みかん先生

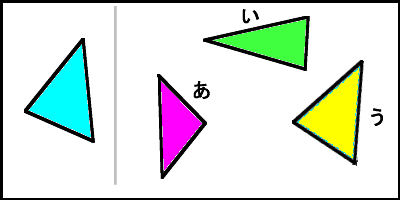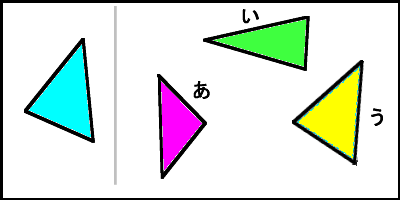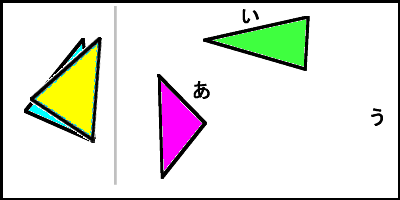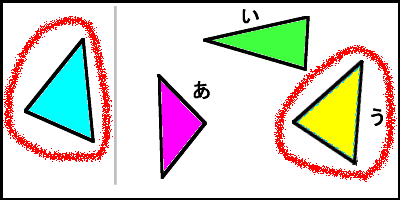
５年算数合同な図形 わかる教え方

無料 中２数学 標準問題 解答プリント 227 図形７ 復習

小学５年生の算数 合同な図形の性質を知る 練習プリント ちびむすドリル 小学生

５年生算数 図形の角 導入 指導実践 Keynoteを使ってテンポよく ネコ好きな学校の先生の日常

小学５年生の算数 合同な図形を見分ける かく 練習プリント ちびむすドリル 小学生

ボード 学習 のピン

中学2年 数学 合同な図形とは Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト

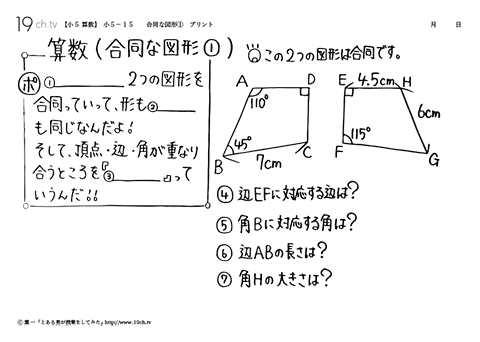
小学5年生の算数 動画 合同な図形 の問題 19ch

合同な図形の性質 三角形の合同とはどういう意味 Qikeru 学びを楽しくわかりやすく

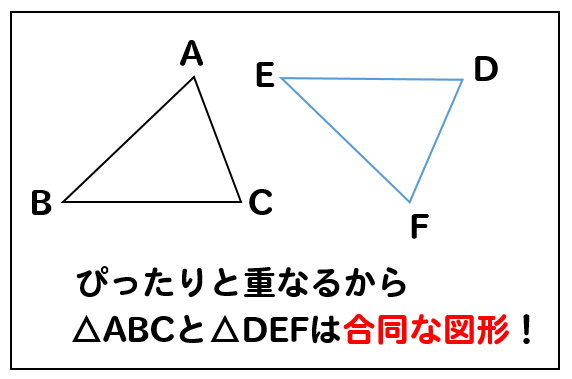
中学数学 合同な図形の性質とは 見つけ方は 問題を使って解説 数スタ

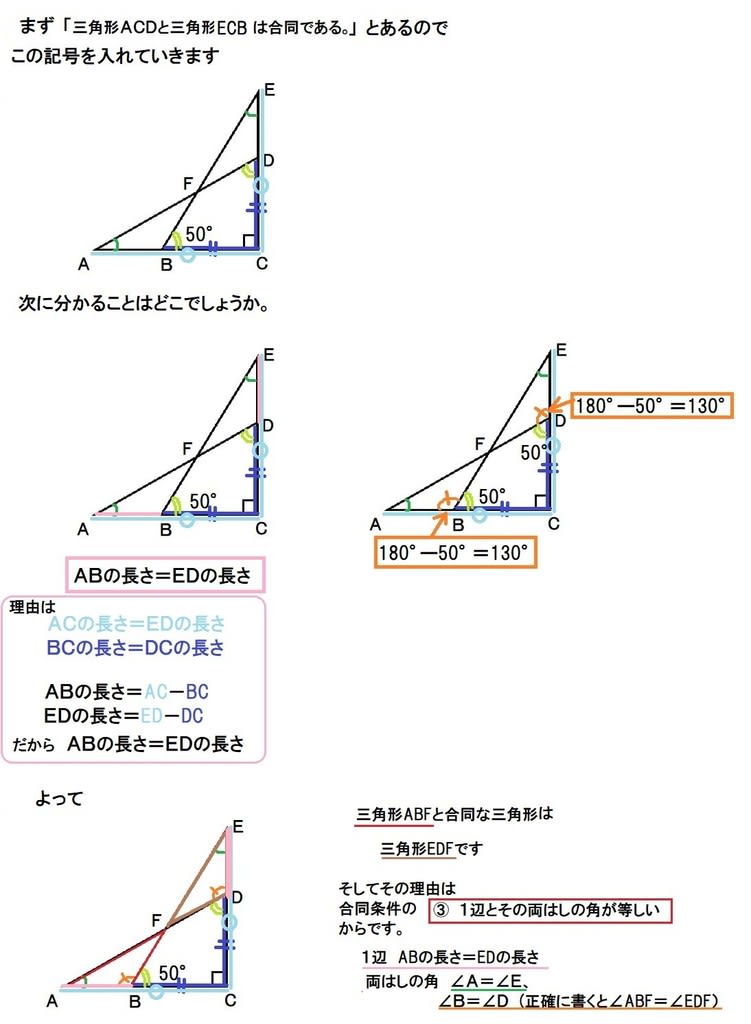
合同な図形 小５ 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support

1

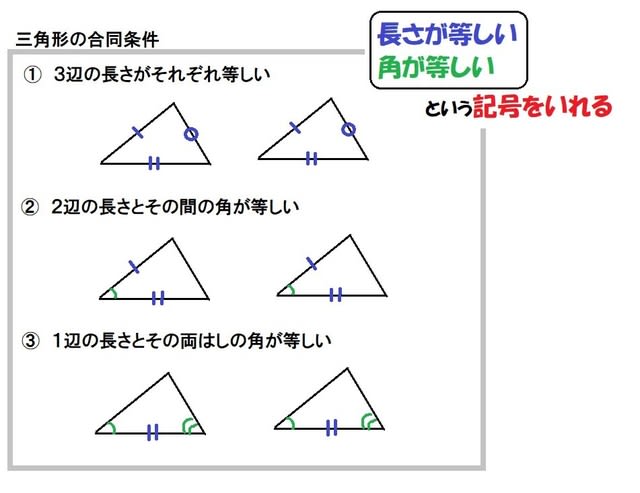
合同な図形 小５ 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support

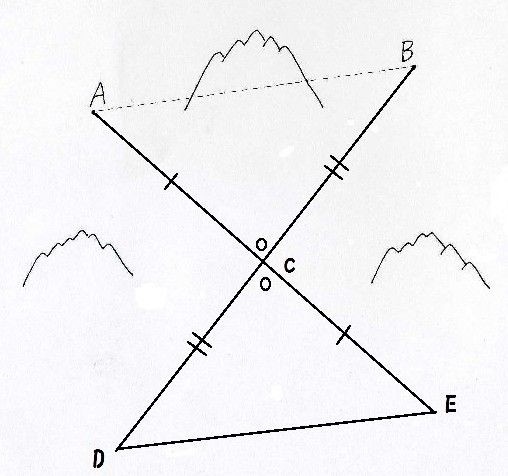
5年算数 合同な図形 ゲンタの授業ポートフォリオ

世界一分かりやすい算数 小５ 合同な図形

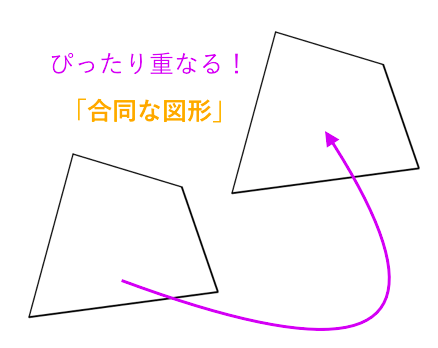
合同な図形とは 苦手な数学を簡単に

Iwate U Repo Nii Ac Jp Action Repository Uri Item Id 140 File Id 36 File No 1

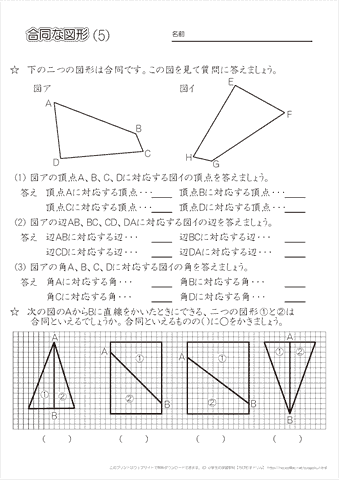
小学５年生の算数 合同な図形の性質を知る 練習プリント ちびむすドリル 小学生

Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S5 024 Pdf

平面図形の良問 合同な三角形 灘中学校12年 理系のための備忘録

世界一分かりやすい算数 小５ 合同な図形

すきるまドリル 小学５年生 算数 合同な図形 無料学習プリント すきるまドリル 無料学習プリント

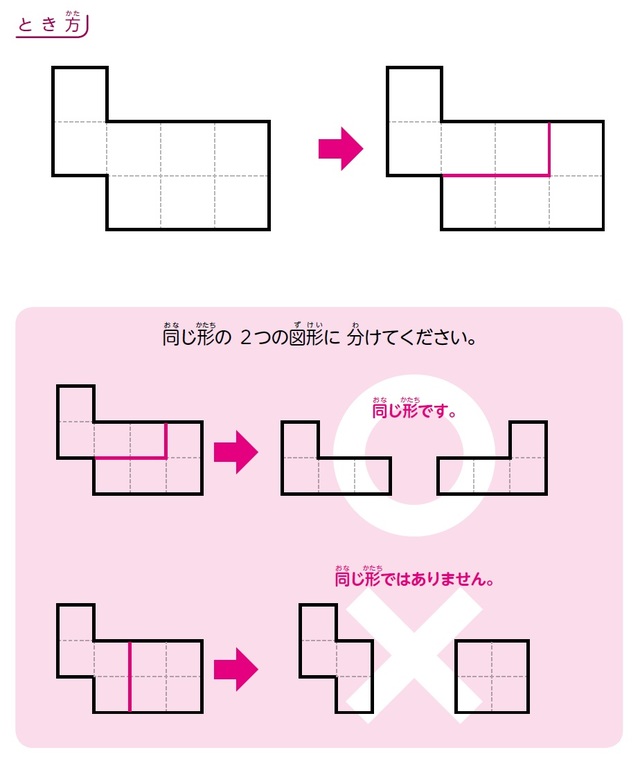
パズル 1つの図形から同じ形を2つ作ろう 合同分割の問題 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン

合同4分割問題できますか 恋する中高一貫校 適性検査 徹底攻略

旧バージョン 5年算数 図形の角と合同 ４ 合同な三角形をかこう Youtube

無料 中２数学 標準問題 解答プリント 225 図形５ 仮定と結論

世界一分かりやすい算数 小５ 合同な図形

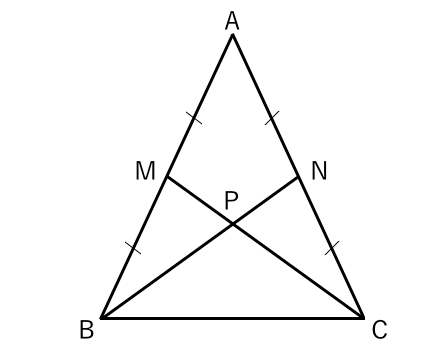
合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に

Tossランド ５年生 第３時 合同な図形 全4時

合同な三角形の作図 2つの辺とその間の角 スクールプレゼンター用教材 教材 プリント 学びの場 Com

1

式と計算 テストの前に

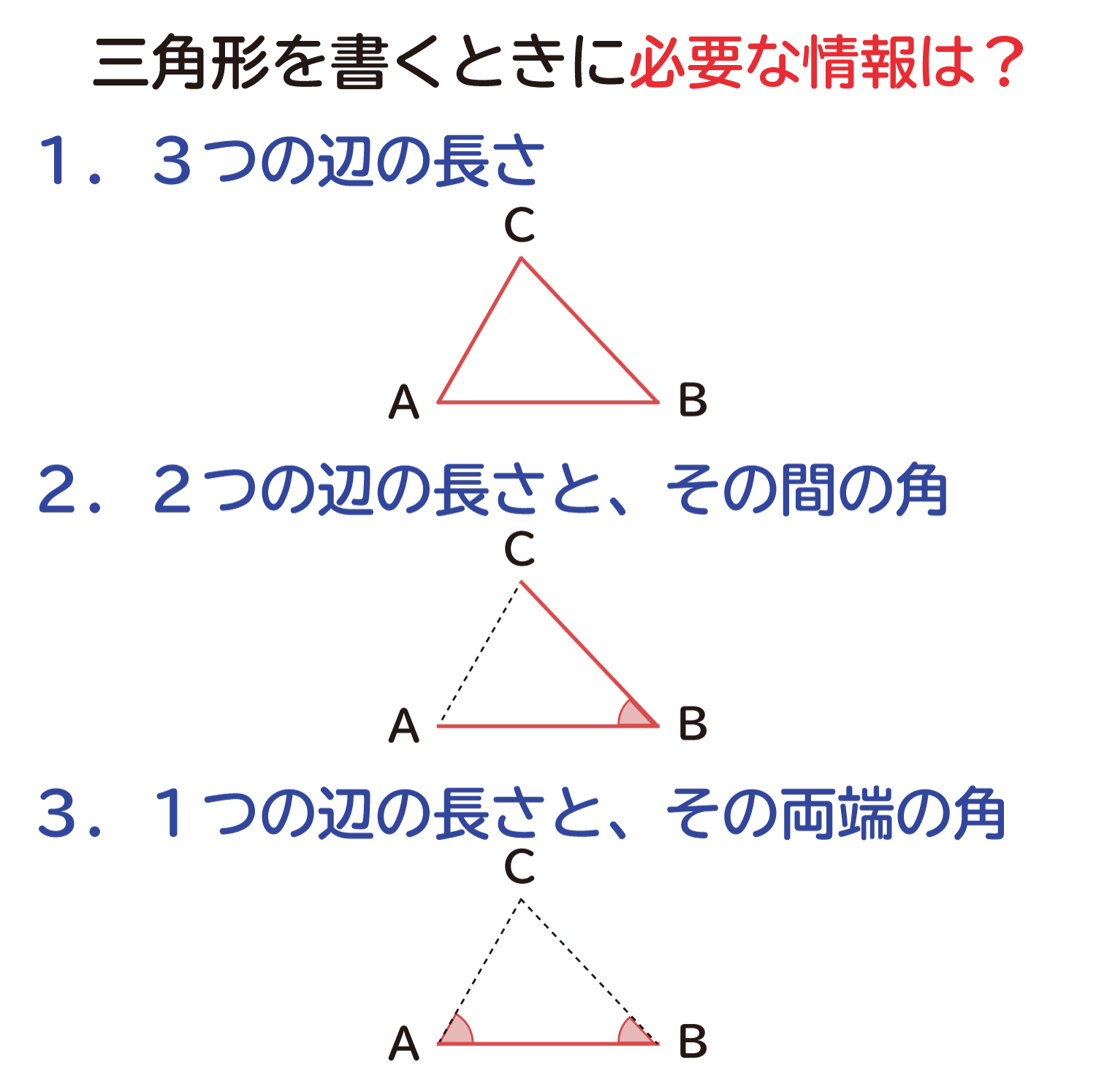
三角形の合同条件の説明 おかわりドリル

世界一分かりやすい算数 小５ 合同な図形

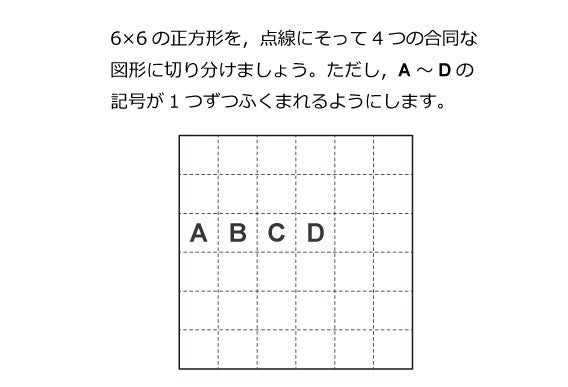
合同な図形に切る 算数パズル 受験算数に挑戦

オンライン授業 小学校５年生算数 合同な図形の対応する頂点 辺 角 Youtube

中2数学 三角形の証明の仕方 Pikuu

合同な図形 あれ を生み出すアイディア教材

世界一分かりやすい算数 小５ 合同な図形

図形が不得意な子は 高度な図形問題 を解くときこの３点を気をつけよう 算数数学が苦手な子専門のプロ家庭教師みかん先生

中２数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾

小学5年生の算数 動画 合同な図形 の問題 19ch

小学5年生 合同な図形の問題プリント まとめテスト 無料の塾プリント

合同 算数星人のweb問題集 中学受験算数の問題に挑戦

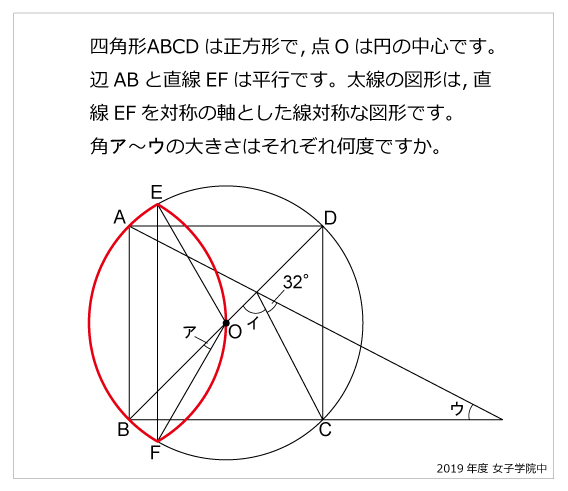
合同 算数星人のweb問題集 中学受験算数の問題に挑戦

小5算数 合同な図形 指導アイデア みんなの教育技術

世界一分かりやすい算数 小５ 合同な図形

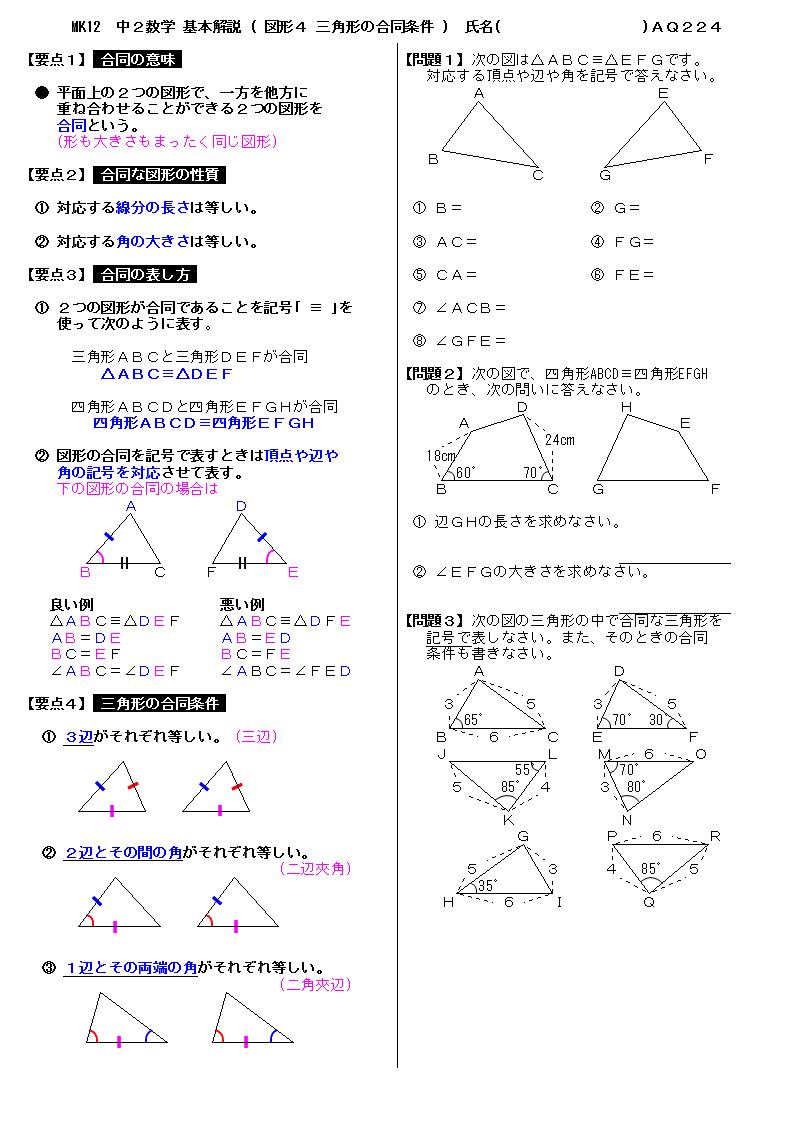
無料 中２数学 基本解説 問題プリント 224 図形４ 三角形の合同条件

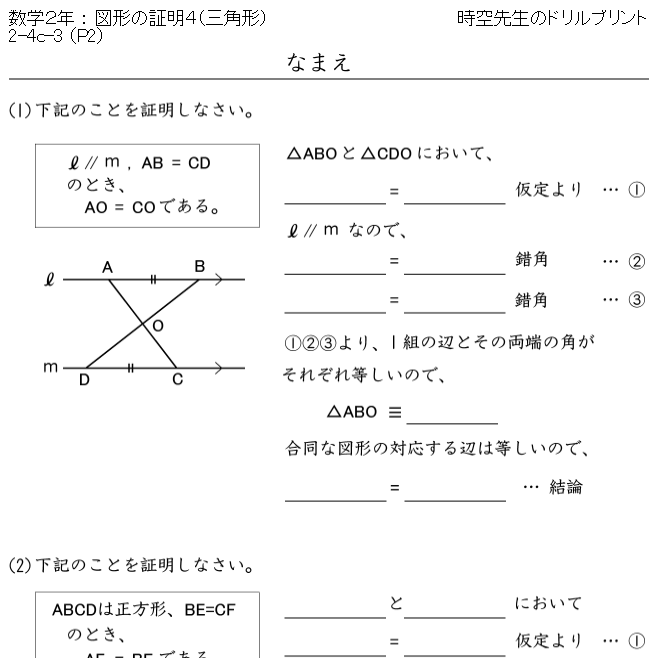
合同な図形の証明練習 個人塾 個人指導の教材

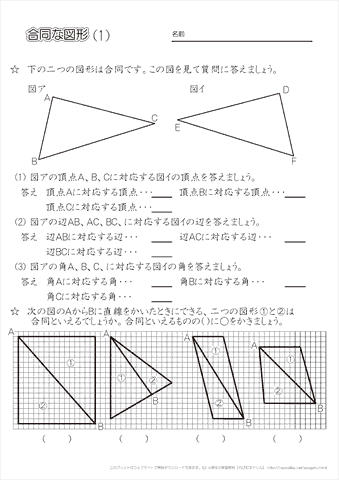
小学５年生の算数 合同な図形の性質を知る 練習プリント ちびむすドリル 小学生

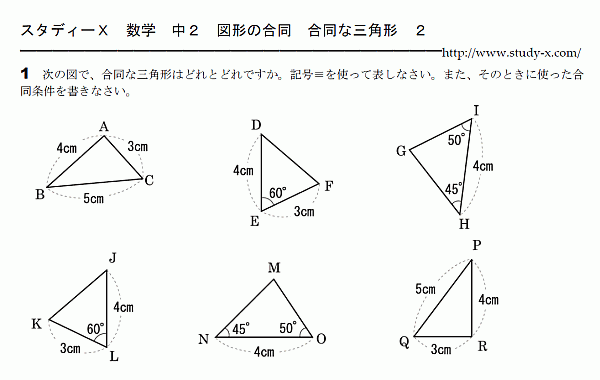
中2 数学 無料学習プリント教材

世界一分かりやすい算数 小５ 合同な図形

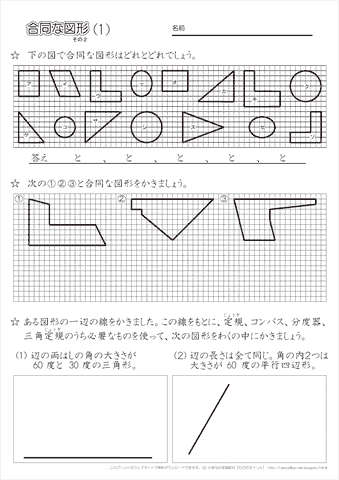
小学５年生の算数 合同な図形を見分ける かく 練習プリント ちびむすドリル 小学生

小学5年生の算数 合同な図形 について教えてください 画像添付の問題なのですが Yahoo 知恵袋

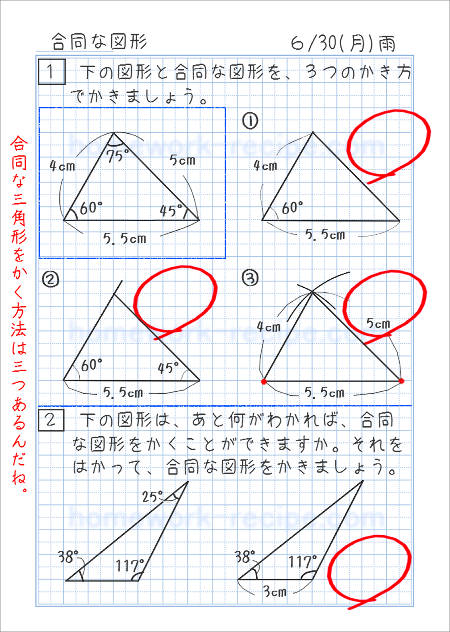
合同な三角形をかこう 家庭学習レシピ

1

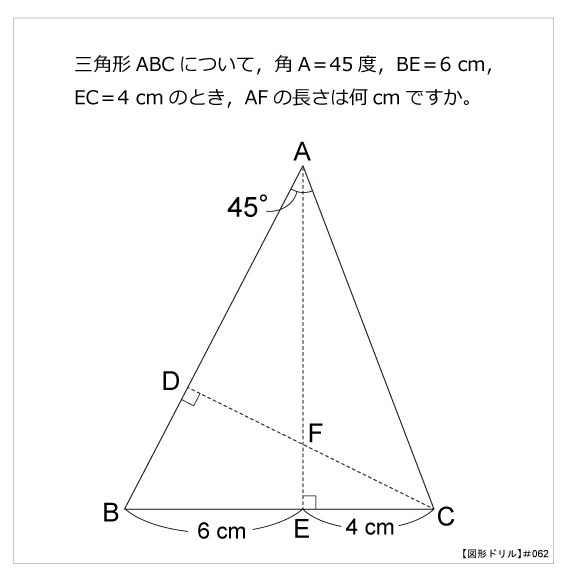
図形ドリル 第62問 合同の発見 算数星人のweb問題集 中学受験算数の問題に挑戦

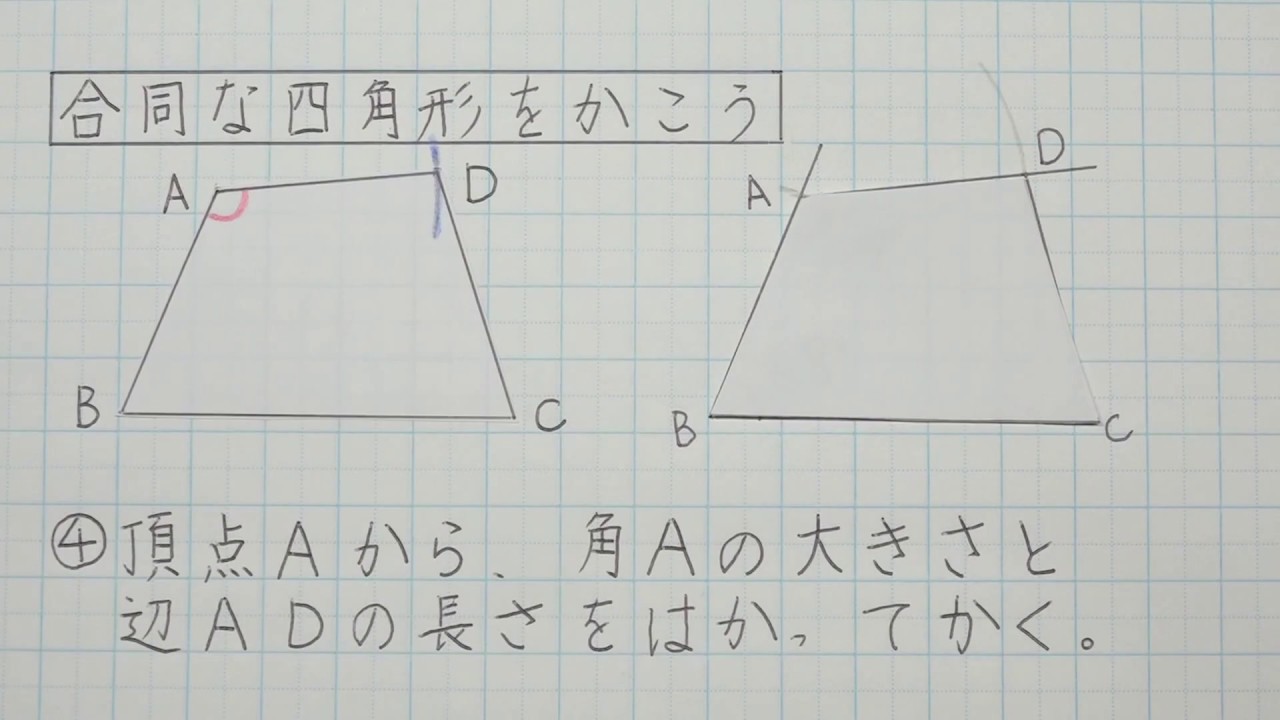
5年算数 図形の角と合同 ５ 合同な四角形をかこう Youtube

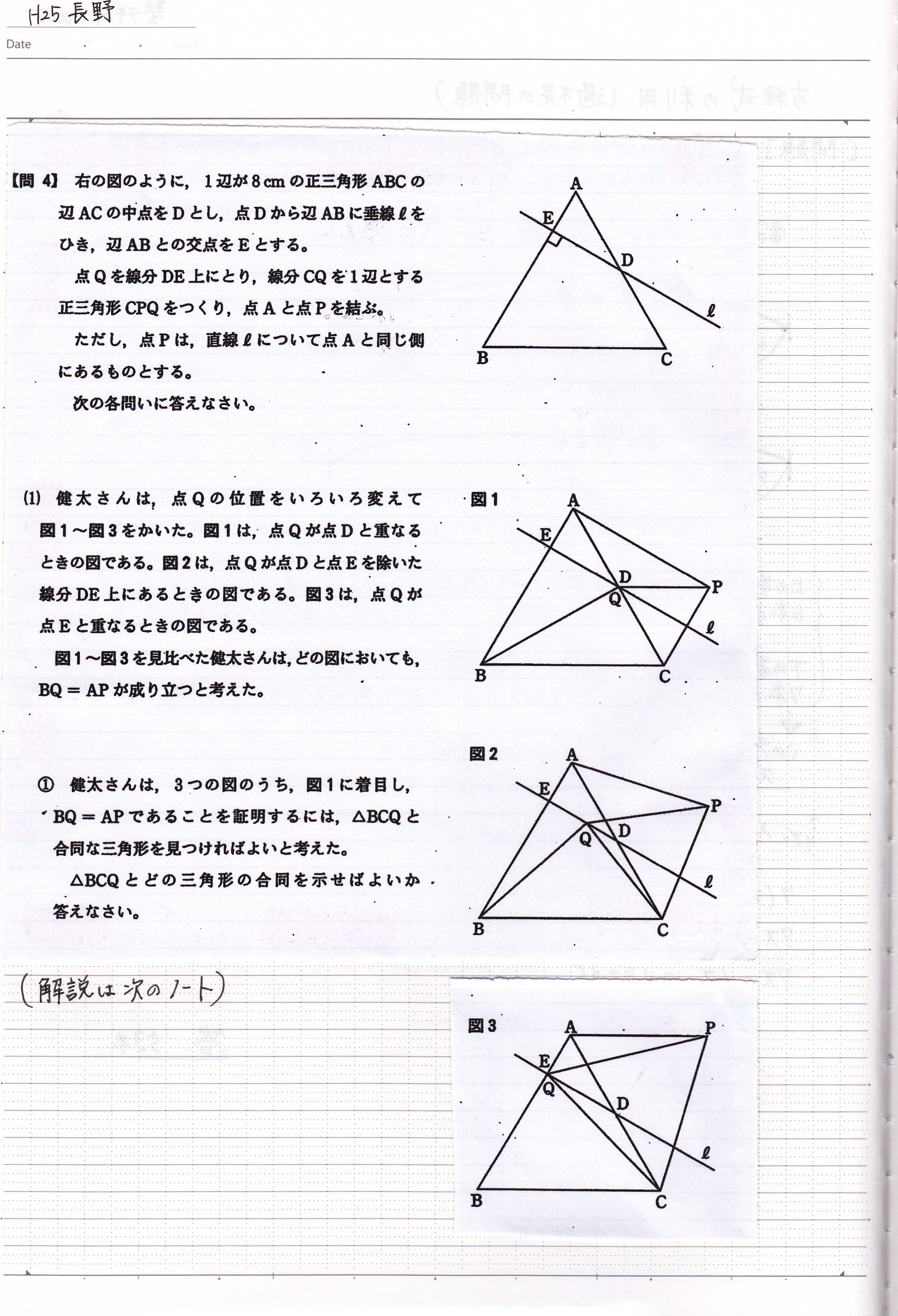
平成25年長野県立高校 入試問題 図形の問題 合同な図形を探す 現役塾講師のわかりやすい中学数学の解き方

合同と証明 Ict教材eboard イーボード

対称な図形 たしかめよう ６年生 翁島 おきなしま 小学校ホームページ

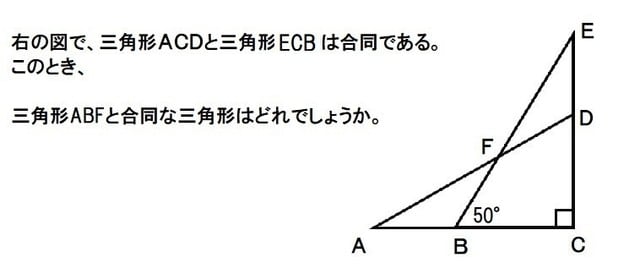
合同な図形 小５ 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support

５年算数合同な図形 わかる教え方

世界一分かりやすい算数 小５ 合同な図形

小学校５年 合同な図形を探そう 問題編 パパしゅくとコラボしたよ Youtube

三角形の合同条件 合同な図形の見つけ方 証明問題の基礎を身につけよう 数スタ

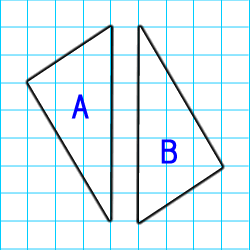
小学 ５年生 算数 合同な図形 演習 問題１

中2 数学 無料学習プリント教材

合同な図形の性質 三角形の合同とはどういう意味 Qikeru 学びを楽しくわかりやすく

Studydoctor合同な図形とは 中２数学 Studydoctor

世界一分かりやすい算数 小５ 合同な図形

小５ 算数 小５ １５ 合同な図形 Youtube

合同な図形 は色わけとマス数えで確かめよう 図式

小学５年生 算数 7月 合同な図形 三角形と四角形の角度 偶数と奇数 倍数と公倍数 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ

Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 合同の証明 働きアリ

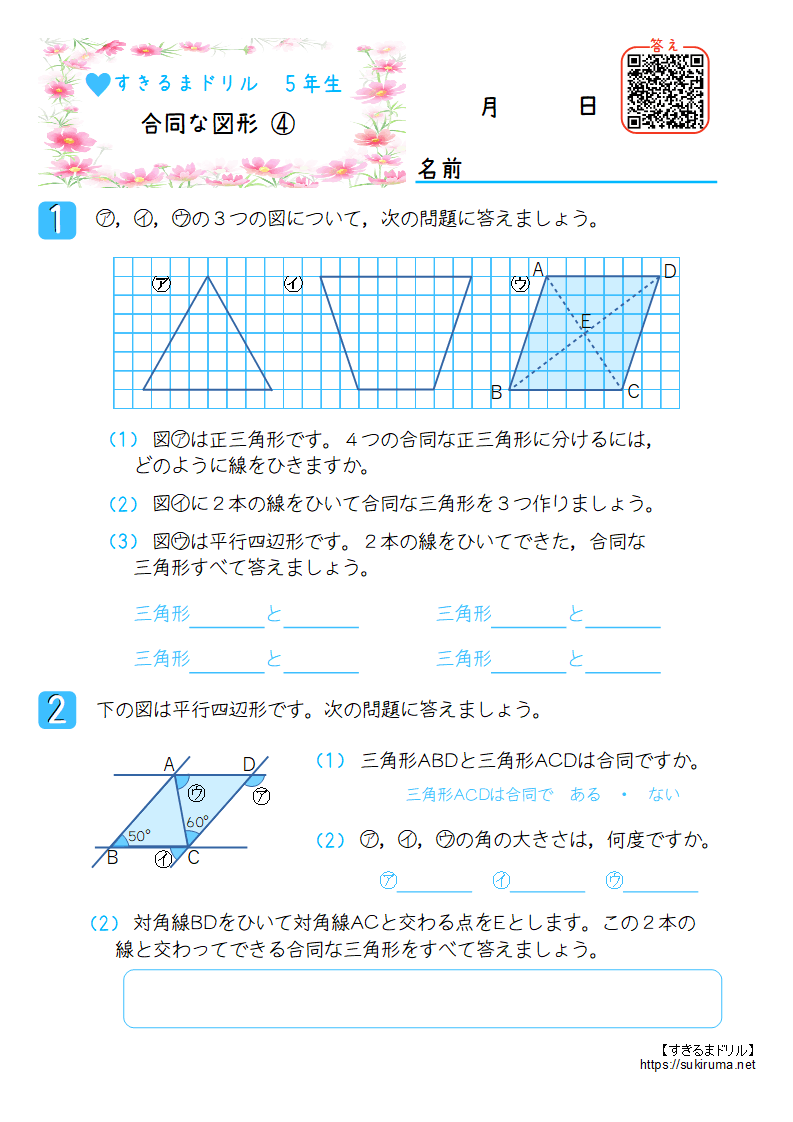
すきるまドリル 小学５年生 算数 合同な図形 無料学習プリント すきるまドリル 無料学習プリント

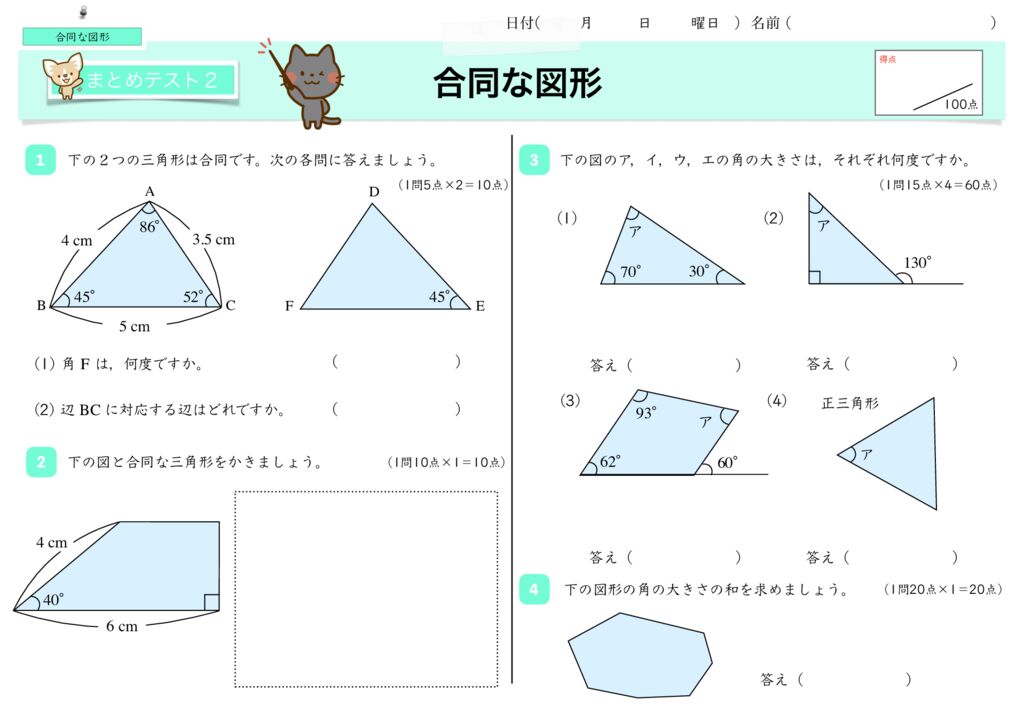
世界一分かりやすい算数 小５ 合同な図形

子どもたちのお勉強の様子です 2年生算数 数の大小 3年生算数 数の表し方 5年生算数 合同な図形 New 中津市立真坂小学校

すきるまドリル 小学５年生 算数 合同な図形 無料学習プリント すきるまドリル 無料学習プリント

合同な三角形をかこう 家庭学習レシピ

1

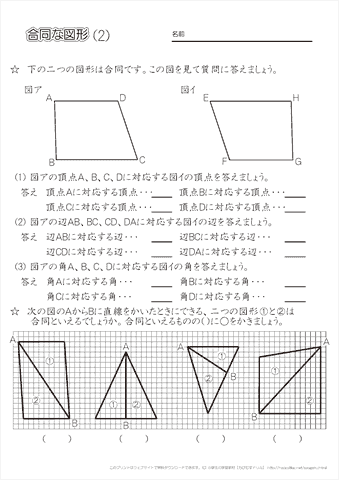
小学５年生の算数 合同な図形の性質を知る 練習プリント ちびむすドリル 小学生

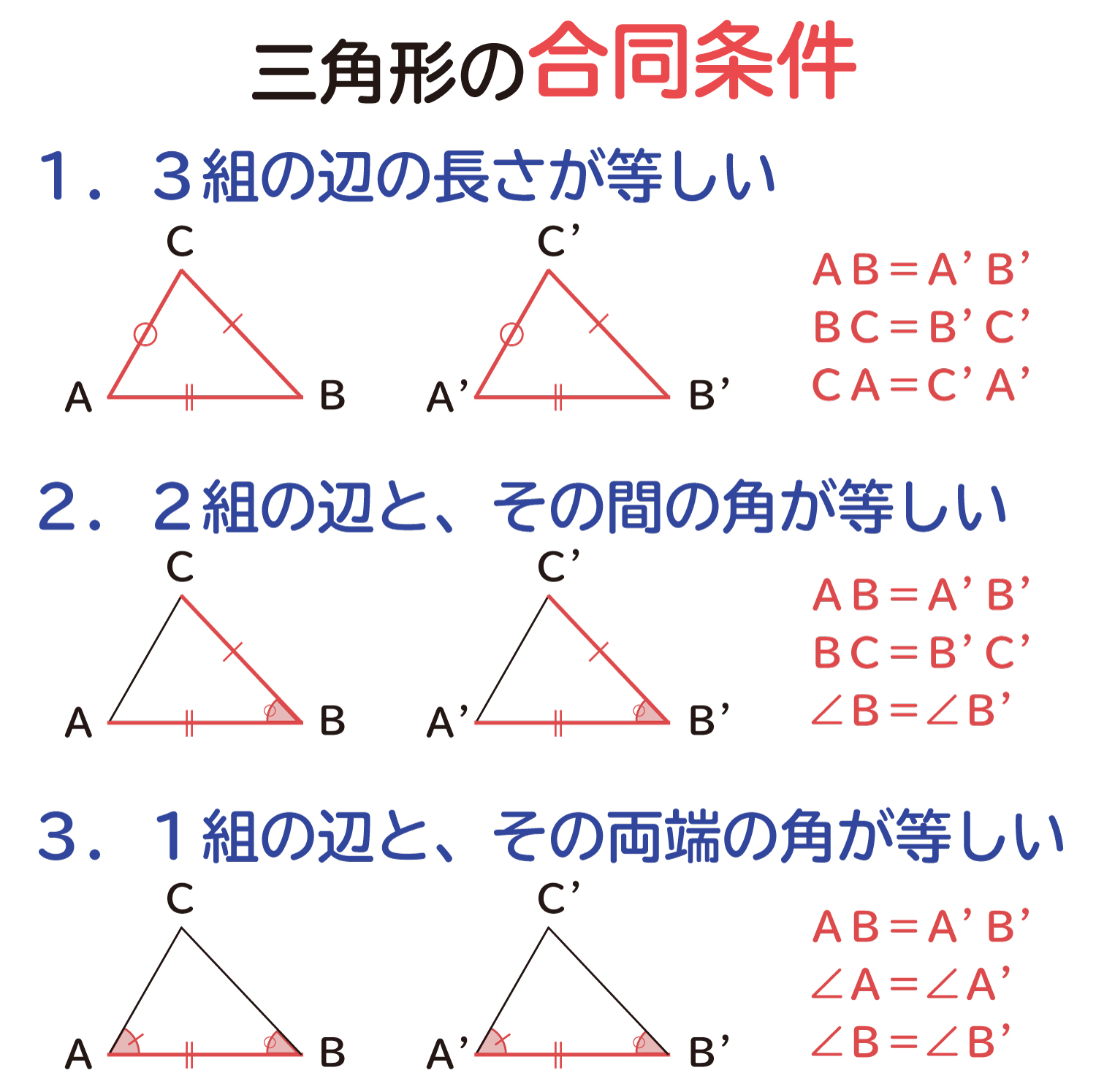
三角形の合同条件の説明 おかわりドリル

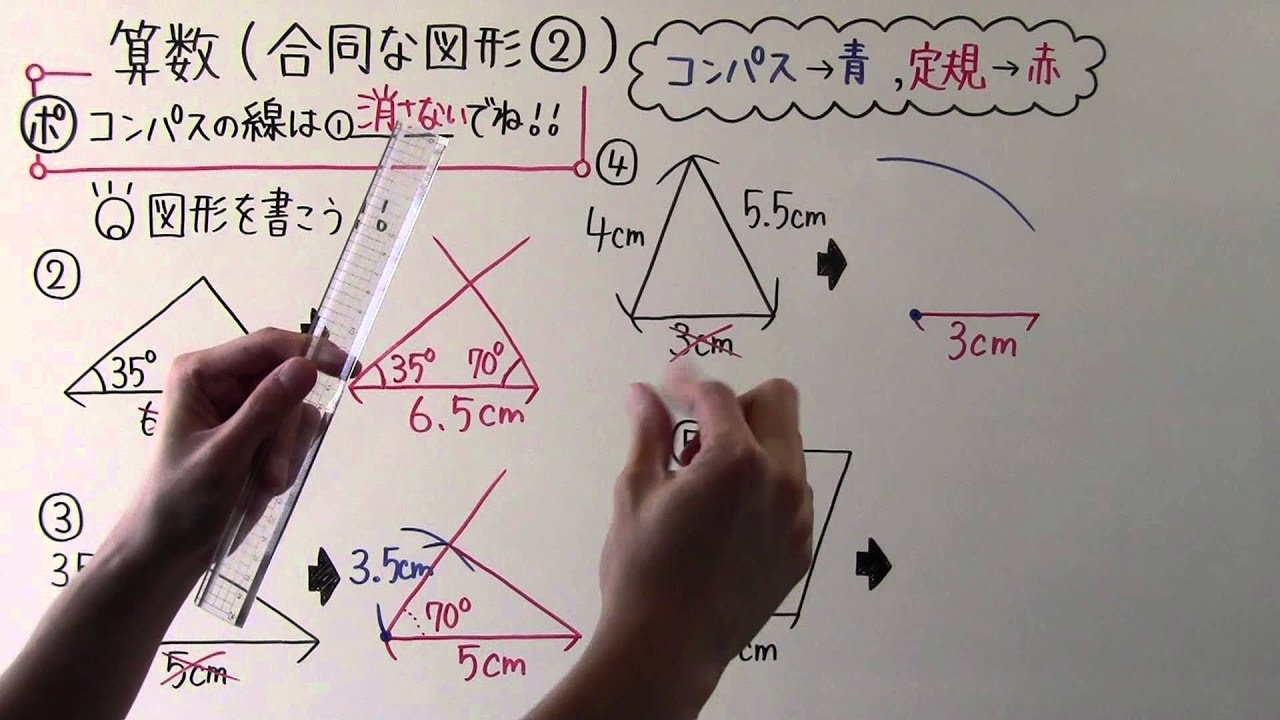
小５ 算数 小５ １６ 合同な図形 Youtube

５年算数 合同な図形 かき方のワークシートです ネコ好きな学校の先生の日常

証明の書き方 合同な三角形の証明問題のかき方を基礎から解説 数スタ

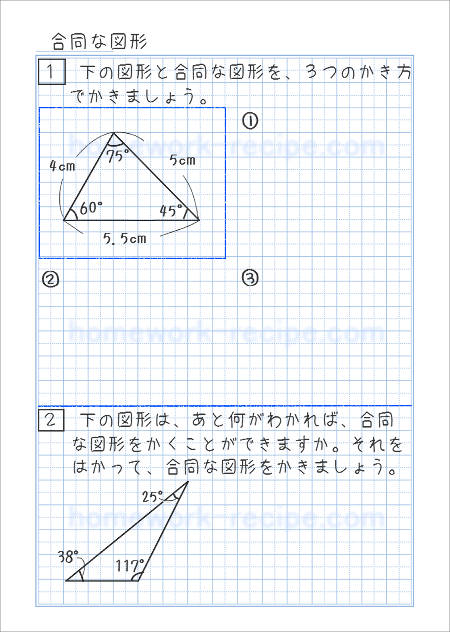
合同な三角形をかこう 家庭学習レシピ

合同な図形 内角 Ict教材eboard イーボード

Incoming Term: 合同な図形 問題,